## §4.2 指数函数及其性质

## (第一课时)

## 课堂引入: 1、我们来看一个生物学问题: 某种细胞分裂，第一次分裂由 1 个分裂成 2 个，第二次分裂由 2 个分裂成 4 个，第三次分裂由 4 个分裂成 8 个，……那么第 $x$ 次分裂变成的细胞个数 $y =$ ___.

2、我们再看一个语文问题： 《庄子·天下篇》中写道：“一尺之棰，日取其半，万世不竭”，请写出取 $x$ 次后，木棰的剩余量 $y =$ ___.

3、通过上面两个问题，我们得到了两个 $y$ 关于 $x$ 的表达式： $y = {2}^{x}$ ， $y = {\left( \frac{1}{2}\right) }^{x}$ ，这就是我们本节课需要研究的指数函数.

## 要点 1: 指数函数的概念 形如___ $\left( {a > 0\text{ 且 }a \neq 1}\right)$ 的函数叫做指数函数.

注：① $a$ 叫做指数函数的底数，规定： $a > 0$ 且 $a \neq 1$ ；

②形式上的严格性： ${a}^{x}$ 的系数为 1，后面不能加式子或常数， $x$ 也不能加常数.

## 题型一：指数函数的概念 例 1: 下列函数中，哪些是指数函数? (1) $y = {4}^{x}$ ； (2) $y = {x}^{4}$ (3) $y = - {4}^{x}$ ； (4) $y = {2}^{-x}$ ； (5) $y = {\left( \frac{1}{2}\right) }^{2x}$ ; (6) $y = {2}^{x + 1}$ ； (7) $y = {\left( 2a - 1\right) }^{x}\left( {a > \frac{1}{2}\text{ 且 }a \neq 1}\right)$ 练习 1: (1) 若函数 $y = \left( {{a}^{2} - {3a} + 3}\right) \cdot {a}^{x}$ 是指数函数，则有（ ） A. $a = 1$ 或 $a = 2$ B. $a = 1$ C. $a = 2$ D. $a > 0$ 且 $a \neq 1$ （2）若指数函数 $y = f\left( x\right)$ 的图象经过点 $\left( {2,4}\right)$ ，则求 $f\left( {-1}\right) =$ ___. ## 要点 2：指数函数的图象和性质 请利用列表描点法画出指数函数 $y = {2}^{x}$ 的大致图形： <!-- Media -->

$x$	-100	-5	-2	0	3	10
$y$

<!-- Media --> 通过图象能观察出 $y = {2}^{x}$ 的哪些性质呢? 请问：通过 $y = {2}^{x}$ 的图象，能够直接得到指数函数 $y = {\left( \frac{1}{2}\right) }^{x}$ 的图象吗? 总结：指数函数 $y = {a}^{x}\left( {a > 0\text{ 且 }a \neq 1}\right)$ 的图象和性质如下： <!-- Media -->

	$0 < a < 1$	$a > 1$
图象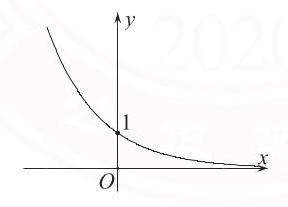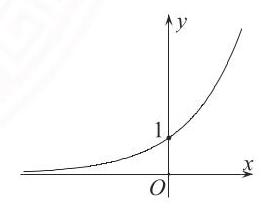
定义域
值域
定点	请问：函数 $y = {a}^{x + 2} - 1$ 过定点___.
单调性
对称性	底数互为倒数的两个指数函数 $y = {a}^{x}$ 与 $y = {\left( \frac{1}{a}\right) }^{x}$ 的图象 关于___对称.
满足抽象函数关系

<!-- Media --> ## 二: 指数函数的图象 例 2: 如图所示，曲线 ${C}_{1},{C}_{2},{C}_{3},{C}_{4}$ 分别是指数函数 $y = {a}^{x},y = {b}^{x},y = {c}^{x},y = {d}^{x}$ 的图象, 则 $a,b,c,d$ 与 1 的大小关系是___. <!-- Media --> <!-- figureText: y↑
${C}_{3}$
${C}_{4}$
0
$\overrightarrow{x}$ --> <!-- Media --> 练习 2: (1) 函数 $y = {a}^{x} - \frac{1}{a}\left( {a > 0,a \neq 1}\right)$ 的图象可能是 ( ) <!-- Media --> <!-- figureText: Ay
0
$x$ --> A. <!-- figureText: Ay --> B. <!-- figureText: Ay
0 --> C. <!-- figureText: Ay
o --> D. <!-- Media --> （2）已知实数 $a,b$ 满足等式 ${\left( \frac{1}{2}\right) }^{a} = {\left( \frac{1}{3}\right) }^{b}$ ，有下列 5 个关系式： ① $0 < b < a$ ② $a < b < 0$ ③ $0 < a < b$ ④ $b < a < 0$ ⑤ $a = b$ ，其中可能成立的有___. ## 题型三：利用指数函数的单调性比较大小 例 3: 比较下列各组数的大小. (1) ${\left( \frac{3}{4}\right) }^{-{1.8}}$ 与 ${\left( \frac{3}{4}\right) }^{-{2.6}}$ （2） ${\left( \frac{5}{8}\right) }^{-\frac{2}{3}}$ 与1； (3) ${0.6}^{-2}$ 与 ${\left( \frac{4}{3}\right) }^{-\frac{2}{3}}$ ; (4) ${\left( \frac{1}{3}\right) }^{0.3}$ 与 ${3}^{-{0.2}}$ . 练习 3: (1) 已知 $a = {0.8}^{0.7},b = {0.8}^{0.9},c = {1.2}^{0.8}$ ，则 $a,b,c$ 的大小关系是___. （2）比较 $a = \sqrt[4]{24},b = \sqrt[3]{12},c = \sqrt{6}$ 的大小关系是___.